【ゼロからのYOLO解説】3. YOLOネットワーク

こんにちは、人です。

今回はYOLOネットワークの解説を行っていきます。

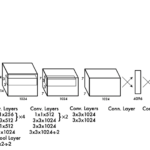
以下の画像において右側の部分がYOLOネットワークですね。

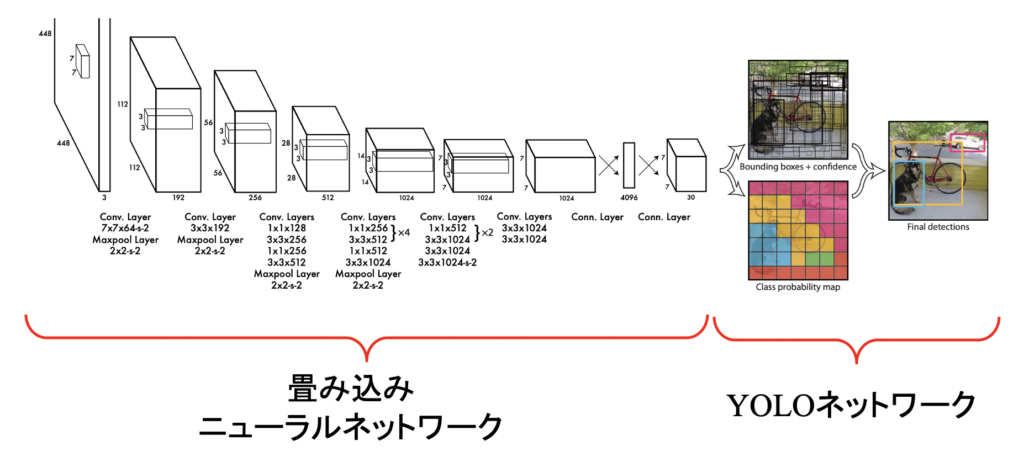
また、YOLOの論文では以下の式が出てきます。👇

$$Pr(Class_i|Object) * Pr(Object) * IOU^{Truth}_{Pred} = Pr(Class_i) * IOU^{Truth}_{Pred}$$

できるだけ図を使って感覚的に分かるようにしようと思っていますが、

こちらの式についても言及していこうと思います！

YOLOネットワークではConfidence Scoreを求めていますが、

ここでは、分かりやすいようにYOLOネットワークを5段階に分割して考えます。👇

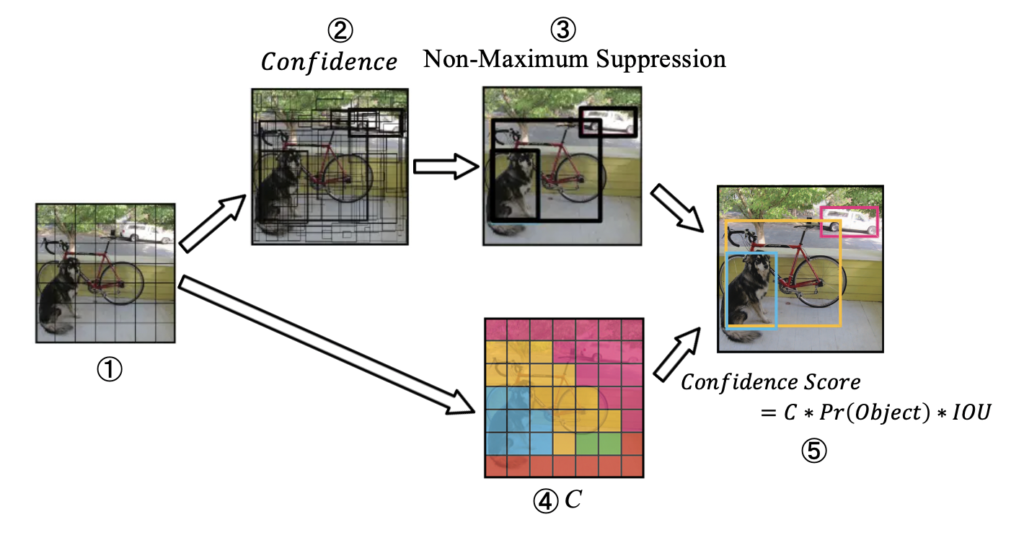
①入力

前回の復習になりますが、CNNの出力を以下に示します。👇

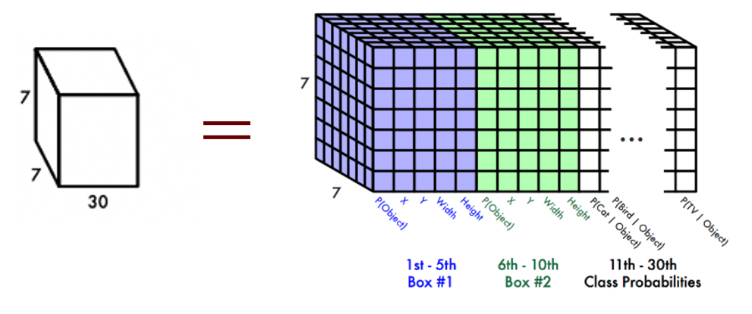
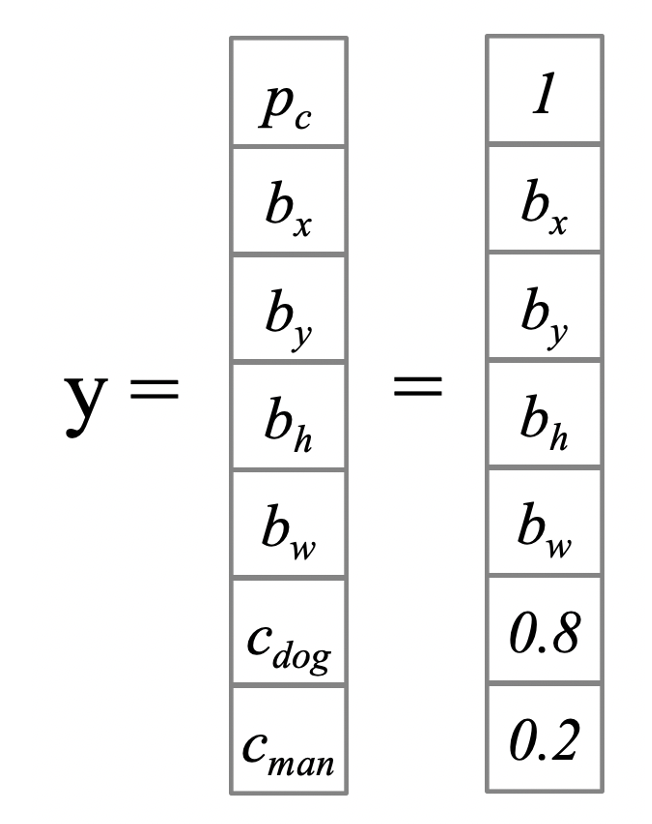
この一つのグリッドには以下のような情報が入っていましたよね👇

＊）今回は簡略化のために\(c_{dog}\)と\(c_{man}\)しか入っていません。

②Confidence

まず、Confidenceという値を計算します。計算式は以下のとおりです。

$$Confidence = Pr(Object) * IOU^{Truth}_{Pred}$$

と言われてもよく分からないと思うので、説明図を見ていきましょう！👇

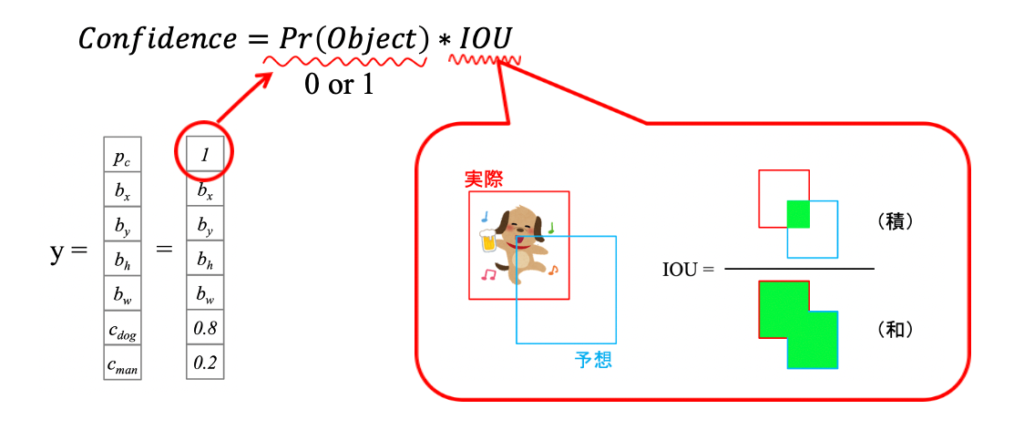
\(Pr(Object)\)は\(p_c\)を表しています。つまり、バウンディングボックスが物体を含んでいれば1になります。（含んでいなければ0ですね）

次に\(IOU^{Truth}_{Pred}\)を見ていきましょう！

まず\(IOU^{Truth}_{Pred}\)とはなんや？という話ですが、\(IOU^{Truth}_{Pred} = Intersection Over Union\)です。Intersectionは積、Unionは和ですので、\(\frac{積}{和}\)ということですね。

上の図のように、可愛いワンコがYOLOアルゴリズムで検出されたとします。

その時、YOLOは水色の枠のようにワンコを予想検出しました。

しかし、実際は赤色の枠で囲われている部分が正解であります。

この時IOUは

$$IOU^{Truth}_{Pred} = \frac{実際と予想の面積の積}{実際と予想の面積の和}$$

ということで、Confidenceをまとめると、

バウンディングボックスに物体が含まれている時の予測検出位置の正確性ということができるのではないでしょうか。

③Non-Maximum Suppression

次にこのNon-Maximum Supressionを説明します！

これは簡単ですのでご安心ください！

検出するバウンディングボックス数を多くすると、下の画像のように一つの物体に複数のバウンディングボックスが検出されるようになります。

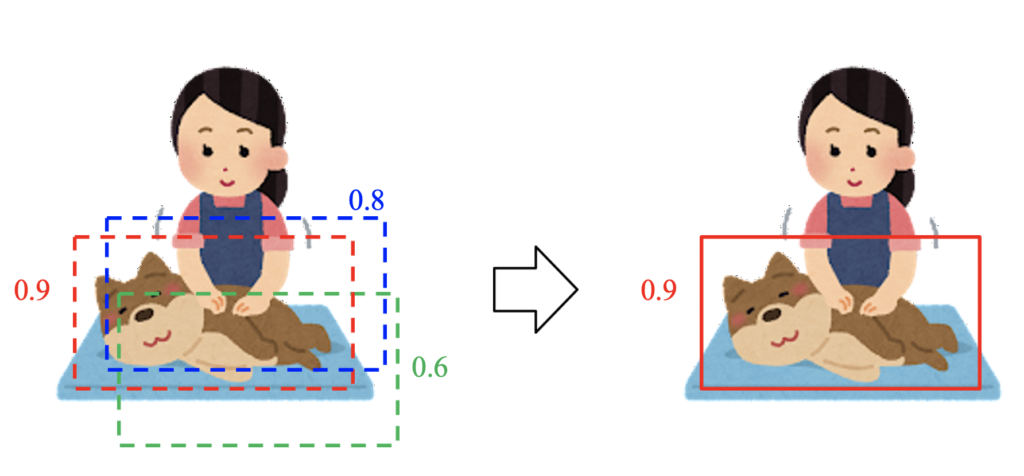
この中で一番IOUの値が高いものを残します。

よって、赤色の枠が採用されるというわけです。

④C

次はCを見ていきましょう！

Cは式でいうと以下のとおりです。

$$C = Pr(Class|Object)$$

画像で言うと以下のやつですね〜

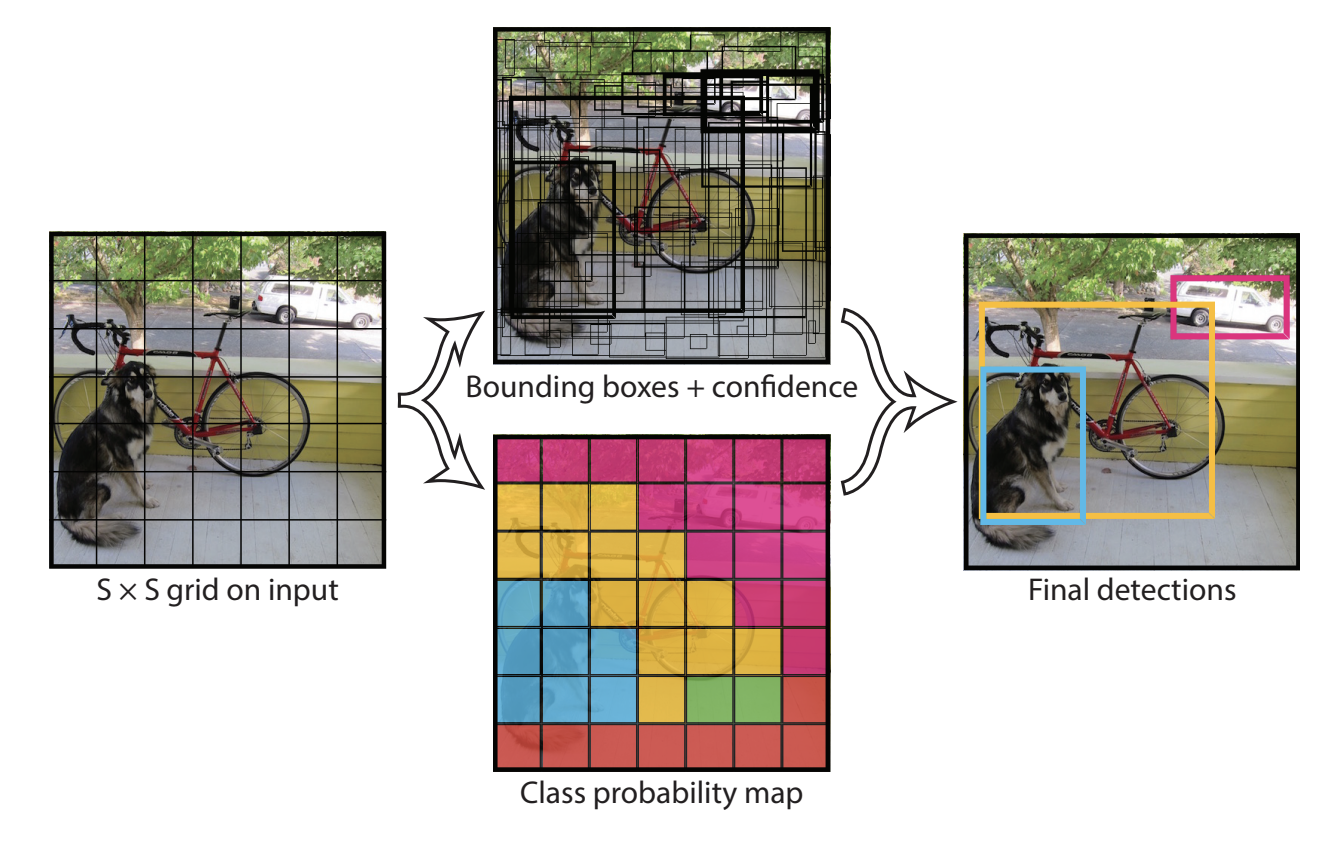
この画像ですよね〜

なんか元画像がグリッドごとに色分けされています。

この色は、「そのグリッド内に最も含まれる物体」を表しています。

画像の例だと、「青 = 犬」、「黄色 = 自転車」、「ピンク = 自動車」、、、と言ったところでしょうか。

では、「グリッド内に最も含まれる物体」をどうやって導き出しているのかというと、、、

以下の図を見てください。👇

\(c_{dog}\), \(c_{man}\)と書いてある部分です。

この\(c\)のなかで最も高い値を持つものを採用するんですね〜

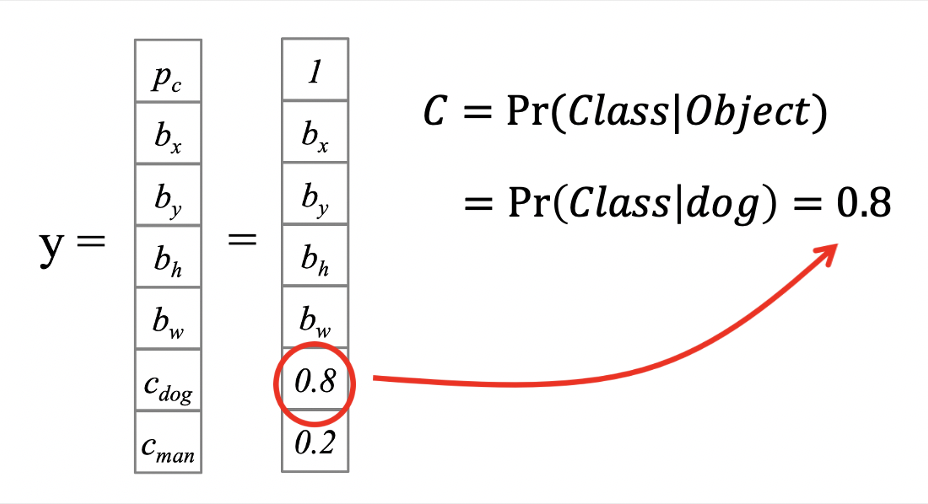
この場合だと、dogが0.8, manが0.2なので、このグリッドに最も含まれている物体は犬であるということになります。

⑤Confidence Score

それでは最後にConfidence Scoreを見ていきましょう！

これは、これまで勉強した\(C\)と\(Confidence\)の積です！

$$Confidence Score = C * Pr(Object) * IoU$$

終わり。